? 13 min
U ovom broju imat ćemo malo nekonvencionalan Uradi sam članak: danas ćeš imati priliku napisati svoj program za simulaciju Galtonove daske. Što je Galtonova daska, zašto je to zanimljivo i kako napisati svoj prvi program – saznaj u današnjem postu.
Pogledaj ovaj video.
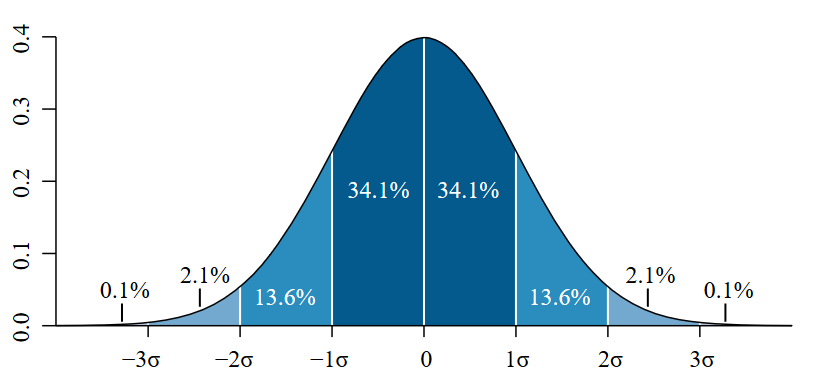
Zrna koja padaju približavaju se normalnoj distribuciji, prikazanoj na slici lijevo. To nije slučajno (ako nisi ubrao/la to iz krivulje na napravi): ova naprava zove se Galtonova ploča i napravio ju je Sir Francis Galton da bi demonstrirao upravo ovu pojavu. Zašto se to događa? I zašto nas je uopće briga? Da bismo odgovorili na ova pitanja, napravimo vlastitu Galtonovu dasku!
Napraviti Galtonovu dasku u stvarnom svijetu traži puno posla. Moja originalna ideja bila je napraviti je od drveta, ali shvatio sam da postoji puno lakši način za demonstrirati ovaj efekt: simulacijom.
Kako bismo ostali vjerni napravi, trebamo pogledati kako ona radi.

Galtonova daska prikazana lijevo ima 13 pretinaca na dnu i 10 redova čavala kroz koje zrna padaju do svojih pretinaca. Kao što vidiš, ima samo jedan način da zrno završi u najdesnijem pretincu (užasno nacrtan narančastom), dok ima mnogo više načina da završi u središnjem pretincu. Udarajući svaki čavao, zrno može ići lijevo ili desno, što u konačnici određuje u koji će pretinac pasti.
Znajući ovo, možemo efektivno simulirati Galtonovu dasku kodom. Da bismo bolje prikazali ovaj efekt, simulirat ćemo dasku koja ima 12 redova čavala, ali možeš se poigrati s kodom da vidiš što možeš napraviti!
Slika lijevo bazirana je na radu korisnika Matemateca na Wikimedia Commons i dijeli se pod CC-BY-SA 4.0.
Da bismo napravili našu simulaciju (i isključivo u svrhu jednostavnosti, vjerujte mi), koristit ćemo programski jezik JavaScript, zajedno s jezikom za dokumente koji se zove HTML. Ugrađeni su u tvoj preglednik, stoga nećeš morati ništa postavljati.
Jedina stvar koju ćeš trebati je uređivač teksta: preporučio bih nešto poput Visual Studio Codea, koji je besplatan i otvorenog koda, ali Notepad (ili TextEdit ili Gedit ako si na Mac ili Linux računalu) također će biti okej ako ti se žuri ili ne možeš instalirati aplikacije. (Vjerojatno bih trebao napomenuti i da vizualni uređivači, poput Worda, neće raditi – treba ti nešto napravljeno za programiranje.)
Za postavljanje naše radne okoline, otvori svoj uređivač teksta i samo spremi praznu datoteku kao Galton.html – tvoj uređivač teksta sad će ti dopuštati da pišeš u novom formatu datoteke zvanom HTML, što je jezik koji se koristi za izradu web stranica.
Možeš otvoriti datoteku u pregledniku da bi pokrenuo web stranicu. Trebaš vidjeti praznu stranicu – to je okej. Ako se pitaš radi li sve kako treba, probaj napisati to u dokument i vidjeti prikazuje li se kad osvježiš stranicu. Kad god nešto promijeniš u svoj HTML datoteci, osvježi stranicu u pregledniku da vidiš promjene.
Izrada sučelja
Ovo je daleko najzahtjevniji i najdosadniji dio izrade ovoga. Ako te ovaj dio ne zanima, osjećaj se slobodno copy-pasteati kȏd ispod i prijeći na pisanje koda koji zapravo simulira nasumičnost. Ako nikad nisi imao/la doticaja s HTML-om i zanima te kako jezik funkcionira, pogledaj ovaj tutorial i vrati se ovamo.
Preskačem preko toga kako HTML funkcionira ovdje, ali trebaš znati osnove:
- stvari u <zagradama> zovu se oznake otvaranja
- stvari u </zagradama> zovu se oznake zatvaranja
- div i span oznake koriste se za sadržavanje drugog sadržaja, što mogu biti druge oznake, objekti ili tekst
- sve oznake čine nešto što se zove stablo dokumenta
- možeš manipulirati stablom dokumenta i mijenjati ga kroz programski jezik JavaScript, što ti omogućuje pisanje aplikacija za preglednike
Ovo je kod koji ćemo sada napisati:
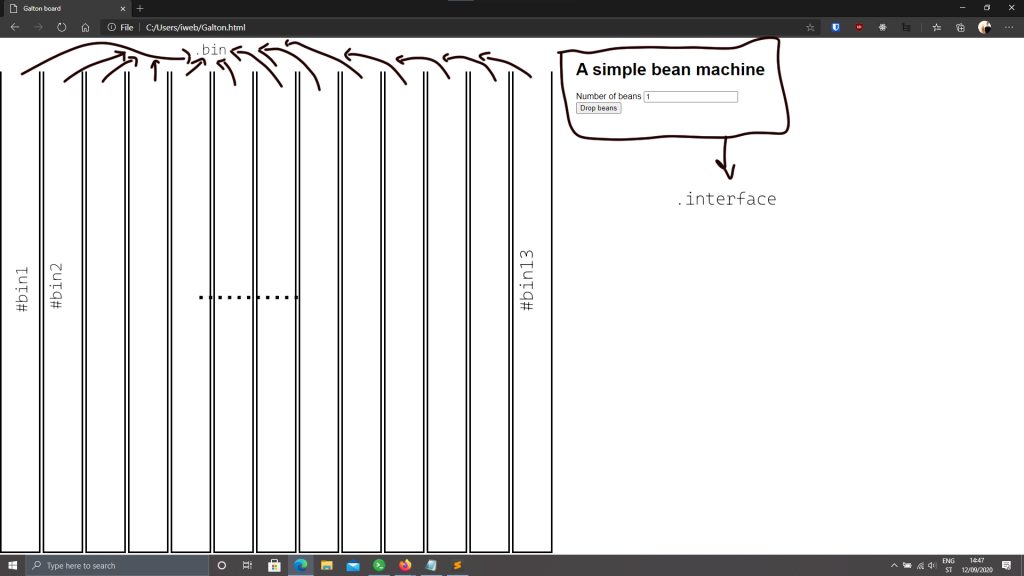
Ovo je sučelje koje ćemo raditi.
Klase koje možemo koristiti da bismo se referencirali na određen tip objekta označene su sa točkom (.) ispred imena, dok su id-jevi koje možemo koristi za referenciranje jednog objekta označeni sa znakom ljestvi (#) ispred njihova imena.
Prvo moramo napraviti osnovnu web stranicu – samo jednostavno sučelje za prikaz rezultata naše simulacije.
Da bismo ovo napravili, počinjemo s pisanjem vrlo jednostavne HTML stranice, koja ne prikazuje i ne radi skoro ništa:
<!DOCTYPE html>
<html>
<head>
<title>Galton board</title>
</head>
<body>
</body>
</html>Stavljat ćemo svoje stilove i skripte u head sekciju, a predložak sučelja stavljat ćemo u body sekciju.
Počnimo sada raditi naše pretnice (koje ću u kodu zvati bins).
Da bismo to napravili, koristit ćemo div elemente (koji su, u HTML-u, samo spremnici za druge elemente).
Unutar naših div elemenata, stavit ćemo prazne span elemente (koji će sadržavati naša zrna). Span element je također samo element-spremnik – nema nikakvog značenja sam po sebi.
Dat ćemo svojim div elementima klasu imena bin kako bismo mogli svim pretncima dati isti stil. Također ćemo im dati i id, kako bismo se mogli referencirati na točno određen spremnik i dobro ga pozicionirati.
Imajući sve to na umu, mogli bismo definirati jedan spremnik ovakvim kodom:
<div class="bin" id="bin1">
<span></span>
</div>Dakle, mogli bismo definirati naših 13 spremnika samo copy-pasteanjem i promjenom id-ja:
<div class="bin" id="bin1">
<span></span>
</div>
<div class="bin" id="bin2">
<span></span>
</div>
<div class="bin" id="bin3">
<span></span>
</div>
<div class="bin" id="bin4">
<span></span>
</div>
<div class="bin" id="bin5">
<span></span>
</div>
<div class="bin" id="bin6">
<span></span>
</div>
<div class="bin" id="bin7">
<span></span>
</div>
<div class="bin" id="bin8">
<span></span>
</div>
<div class="bin" id="bin9">
<span></span>
</div>
<div class="bin" id="bin10">
<span></span>
</div>
<div class="bin" id="bin11">
<span></span>
</div>
<div class="bin" id="bin12">
<span></span>
</div>
<div class="bin" id="bin13">
<span></span>
</div>Sada im trebamo dati nekog stila: možemo napraviti da izgledaju kao spremnici dajući im lijevi, desni i donji rub. Možemo im odrediti i fiksnu širinu, recimo 70px (px ovdje ne znači piksela po definiciji, ali 1px u tvom stilu je približno jednak jednom pikselu na tvom ekranu).
Trebamo im dati i fiksnu visinu. Da bismo napravili sve ovo, treba nam <style> oznaka u našoj <head> sekciji.
<style>
.bin{
width: 70px;
height: 900px;
border-left: 3px solid black;
border-right: 3px solid black;
border-bottom: 3px solid black;
}
</style>Sada trebamo pozicionirati svoje pretince i napraviti da se ne izlijevaju zrna iz njih. Kako ćemo koristiti znak * da bismo predstavili zrno, da bismo spriječili izljevanje, dovoljno je reći našem pregledniku da napravi prijelom ‘riječi’ gdje je potrebno:
<style>
.bin{
width: 70px;
height: 900px;
border-left: 3px solid black;
border-right: 3px solid black;
border-bottom: 3px solid black;
display: inline-block;
position: fixed;
bottom: 3px;
word-break: break-all;
}
</style>Nadalje, da bismo ispravno pozicionirali spremnike, trebamo im dati poziciju. Možemo to učiniti određivanjem svojstva left (koliko je daleko od lijevog ruba ekrana) u oznaci style.
#bin1{
left: 0;
}
#bin2{
left: 80px;
}
#bin3{
left: 160px;
}
#bin4{
left: 240px;
}
#bin5{
left: 320px;
}
#bin6{
left: 400px;
}
#bin7{
left: 480px;
}
#bin8{
left: 560px;
}
#bin9{
left: 640px;
}
#bin10{
left: 720px;
}
#bin11{
left: 800px;
}
#bin12{
left: 880px;
}
#bin13{
left: 960px;
}Konačno, trebamo napraviti da zrna padaju na dno, budući da ne pokušavamo napraviti simulaciju bez gravitacije 🙂 Da bismo to napravili, stavimo ovo u svoju style oznaku – ovaj kod pozicionira naš span element na dno pretinca:
.bin span{
position: absolute;
bottom: 0;
right: 0;
}Sad kad imamo spremnike, trebamo napraviti jednostavno sučelje za upravljanje simulacijom gdje ćemo moći odrediti broj zrna koji ćemo ispustiti i pokrenuti simulaciju klikom na gumb.
Kako bismo to učinili, stavit ćemo div imena klase interface s nekim input elementima za unos. h1 element je naslov za našu stranicu, dok su label i input elementi samodokumentirajući kad im pogledaš atribute. Koristimo br kako bismo prešli u novi red.
<div class="interface">
<h1>A simple bean machine</h1>
<label for="numberOfBeans">Number of beans</label>
<input type="number" value="1" id="numberOfBeans">
<br>
<input type="button" onclick="dropBeans()" value="Drop beans">
</div>Bitan dio ovdje je onclick=”dropBeans()” atribut na gumbu koji kaže pregledniku da pokrene našu simulaciju (napisat ćemo funkciju dropBeans kasnije) kad se klikne na gumb.
Da pozicioniramo svoje sučelje ispravno i kako bi ono malo bolje izgledalo, dodat ćemo ovo u stil – što će dati cijelom dokumentu ljepši font i pozicionirati sučelje na fiksnu poziciju, 20px od vrha i 1080px od lijeve strane ekrana.
body{
font-family: 'Helvetica', 'Roboto', 'Arial', sans-serif;
}
.interface{
position: fixed;
top: 20px;
left: 1080px;
}Naše sučelje sada bi trebalo izgledati ovako:
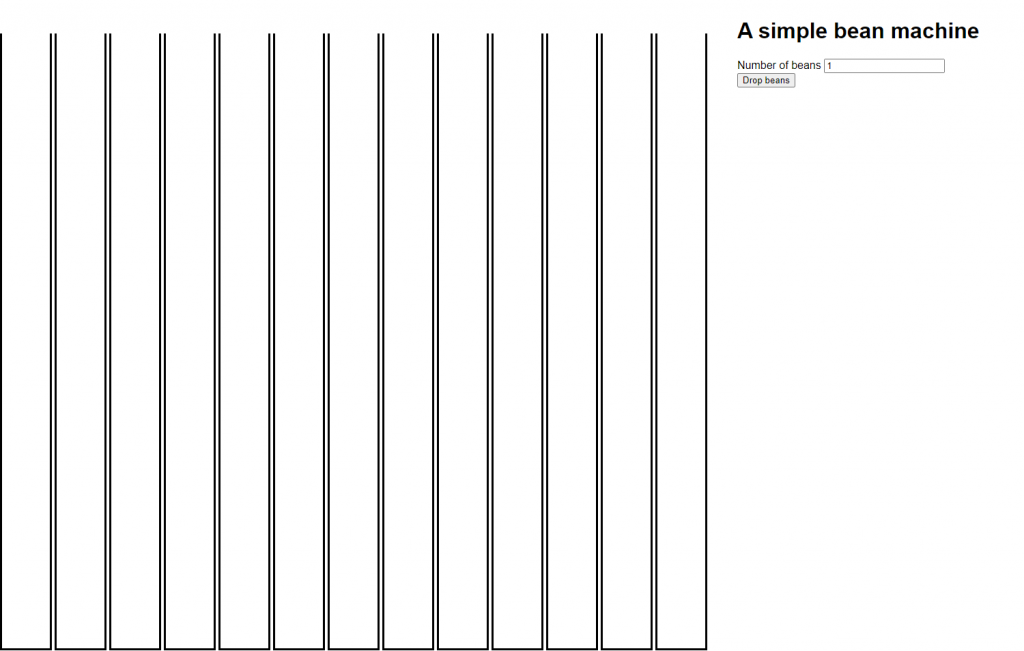
Konačno smo sada gotovi s izradom sučelja: sada trebamo napisati samu simulaciju.
Simulirajmo zrna
Kao što sam već govorio, koristit ćemo JavaScript, jezik ugrađen u preglednike, kako bismo simulirali Galtonovu dasku. Da počneš pisati JavaScript kod, otvori script oznaku u sekciji head ovako:
<script>
</script>Počet ćemo pisanjem jednostavne funkcije koja će ispustiti određen broj zrna u njihove spremnike – spremnik u kojem će završiti svako pojedino zrno odredit će ishod druge funkcije.
Trebamo uzeti vrijednost obrasca – možemo joj pristupiti koristeći document.querySelector(‘#numberOfBeans’).value (što u principu kaže “nađi element s id-jem numberOfBeans u dokumentu i vrati njegovu vrijednost”) – i pokrenuti petlju koja stavlja toliko zrna u pretince.
Kako bismo stavili zrno u pretinac, stavit ćemo samo * u span element u njemu.
Možemo pristupiti internom sadržaju elementa korištenjem document.querySelector(selector).innerHTML i možemo koristiti svojstvo children da bismo pronašli određeno dijete nekog elementa.
Kako je span element jedino dijete spremnika, možemo pristupiti njegovom unutarnjem sadržaju koristeći document.querySelector(‘#bin3’).children[0].innerHTML, čemu možemo dodijeliti i vrijednost.
Naravno, možemo koristiti rezultat izračuna za selektor, stoga document.querySelector(‘#bin’+binToDropIn).children[0].innerHTML također ima smisla.
Da bismo odredili koje zrno upada u koji pretinac, napisat ćemo još jednu funkciju selectBin kasnije, ali ako želiš isprobati radi li ovo, napravi da je dropIn varijabla jednaka broju.
function dropBeans(){
for(var i=0;i<document.querySelector('#numberOfBeans').value;i++){
var dropIn = selectBin();
document.querySelector('#bin'+dropIn).children[0].innerHTML = document.querySelector('#bin'+dropIn).children[0].innerHTML + '*';
}
}Sada trebamo zapravo napisati selectBin funkciju.
Da bismo ostali vjerni napravi, moramo replicirati način na koji funkcionira, a ne njen krajnji rezultat.
U samoj napravi, svako zrno pogodi čavao 12 puta, svaki put skrećući lijevo ili desno. U našem slučaju, počinjat ćemo s krajnje lijevim pretincem (kako bi position=1 sugeriralo) i pokrenuti petlju 12 puta koja može ili pomaknuti zrno desno ili ga ostaviti na istom mjestu.
Da bismo to odredili, koristit ćemo Math.random(), funkciju koja nam daje nasumičan broj iz segmenta [0,1] i napraviti da nam da ili 0 ili 1, što ćemo pribrojiti poziciji. Napravit ćemo da nam vraća cijele brojeve režući decimale, prije čega ćemo normalizirati njene vrijednosti dodajući 0.5 – u principu, zaokružujemo.
function selectBin(){
var position=1;
for(var k=0;k<12;k++){
position+=Math.trunc((Math.random()+0.5));
}
return position;
}Sad kad ovo imamo napisano, gotovi smo. Naša naprava radi!
Možeš ju isprobati ovdje, ali radit će dobro samo ako si na računalu: https://codepen.io/iwebhub/full/ZEWoOdZ
Ako želiš, također možeš pronaći moj izvorni kod ovdje: https://gist.github.com/mbmjertan/6bf218b06fd566c4f07386cbfca38e88
Okej, zašto?
Ispuštanjem tisuća zrna, možemo se zbilja uvjeriti da uistinu njihova distribucija liči na normalnu distribuciju:

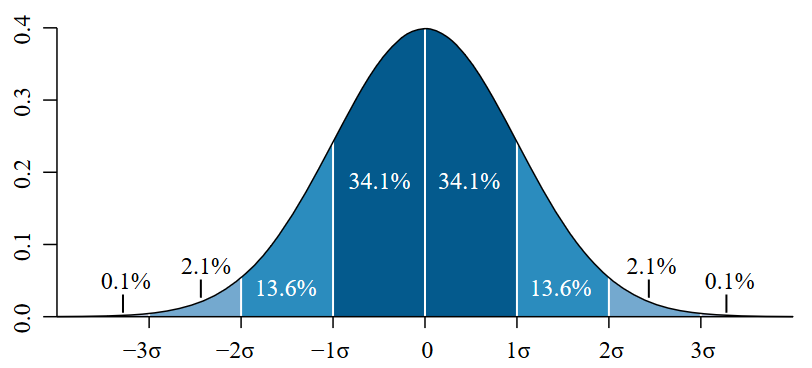
Zašto se ovo događa? I zašto je važno? Da bismo odgovorili na ova pitanja, moramo prvo razumjeti što normalna distribucija (također zvana i Gaussova distribucija) uopće jest.
Ako je probaš naći na Wikipediji, susrest ćeš se s nekim jako preciznim matematičkim definicijama, ali u sažetku, bilo koja distribucija je funkcija vjerojatnosti koja opisuje kako se raspodjeljuju vrijednosti varijable. Ipak, normalna distribucija je malo zanimljivija od toga: to je simetrična distribucija gdje su vjerojatnosti najveće oko središnjeg vrha (što znači da se većina opaženih vrijednosti varijabli događa u tom intervalu) i da se vjerojatnosti za vrijednosti udaljenije od vrha (srednje vrijednosti) smanjuju jednako brzo u oba smjera. Oba ekstrema imaju istu, iako nisku, vjerojatnost. U jednostavnim terminima, ovo znači da su prosječne vrijednosti one najvjerojatnije, dok su one koje značajno odstupaju od toga prosjeka najmanje vjerojatne.
Normalna distribucija pojavljuje se jako puno u stvarnosti, pri čemu su tipični primjeri normalne distribucije visina ljudi, krvni tlak i greške u mjerenjima. Neki testovi su čak dizajnirani da se ocjenjuju koristeći normalnu distribuciju (pri čemu otprilike isti broj ljudi padne ispit kao što ima najveću ocjenu).
Stoga… zašto se pojavljuje ovdje, u scenariju gdje bi varijable trebale biti nasumične?
Pa, prva stvar za uočiti je da, iako je spremnik u koji zrno sleti nasumično određen, nije istinski nasumičan, zato što neki spremnici imaju veću vjerojatnost da budu pogođeni od drugih. Ovo je određeno brojem puteva kojim zrno može doći do spremnika, što sam ilustrirao ranije: ima samo jedan put do krajnje lijevog ili krajnje desnog spremnika, ali ima puno više puteva do središnjih spremnika.
Ako s n označimo broj redova čavala na Galtonovoj dasci, broj puteva do k-tog spremnika na dnu (brojeći k od nule) dan je binomnim koeficijentom n povrh k, koji je jednak n! / (k! * (n-k)!).

Vrijednosti binomnog koeficijenta prikazani su lijevo u Pascalovu trokutu i predstavljaju broj putanji kojima zrno može ići da bi završilo u spremniku na ploči s 8 spremnika i 7 redova čavala.
Ipak, to ne objašnjava posve ovaj fenomen: ove varijable ipak su barem dijelom nasumične – stoga, zašto su normalno distribuirane?
Postoji jako važan teorem u matematici zvan centralni granični teorem koji govori da u nekim (relativno čestim) okolnostima, zbroj mnogo nasumičnih varijabli (poput ovih!) imat će približno normalnu distribuciju. Upravo je ovaj teorem Galton pokušao ilustrirati svojom napravom: broj zrna u spremniku je nasumičan, ali kako se broj diskretnih događaja (ispuštenih zrna) povećava, funkcija počinje nalikovati normalnoj distribuciji!
Iako su razlozi za ovo matematički zahtjevni, pojednostavljena verzija je da kad imaš određenu očekivanu (najvjerojatniju vrijednost) i ponoviš pokus dovoljno puta, većina ishoda će konvergirati k toj vrijednosti, dok će se ostali podjednako proširiti zbog velikog broja pokusa.
Znam, ovi matematički rezultati zvuče jako dosadno, ali zapravo su vrlo važni za naše razumijevanje svijeta oko nas – dajući smisao stvarima koje se čine nasumičnima, poput visina ljudi ili bacanja novčića, čineći ih razumljivijima i predvidljivijima. Na kraju, ovi teoremi mogu se primijeniti u stvarnom svijetu, dajući smisao divljini oko nas, što Sir Francis Galton opisuje sam:
Znam za skoro pa ništa što ima toliku mogućnost impresioniranja mašte kao čudesna forma kozmičkog reda koju izražava “Zakon o frekvenciji greške”.
Zakon bi personificirali Grci i štovali ga, da su znali za njega. Vlada sa spokojem i u potpunoj tajnosti, usred najluđe zbrke. Što je veća gomila i što je golemija prividna anarhija, savršeniji je njegov utjecaj.
On je vrhovni zakon Nerazuma. Kad god se veliki uzorak kaotičnih elemenata uzme u ruke i maršira po redu njihove veličine, neslućeni i najljepši oblik pravilnosti pokaže se cijelo vrijeme latentnim.
Sir Francis Galton o Središnjem graničnom teoremu
Možete li se sjetiti nekih primjera normalne distribucije ili zanimljivu primjenu ovog teorema? Probajte se igrati s našom simulacijom kako biste vidjeli što se događa kad ispustite malen broj zrna, a što kad velik za bolju ilustraciju ovog teorema. Ako imate ikakvih pitanja i ako vam je ovo bilo zanimljivo, ostavite nam komentar ispod.